Zehai's Blog

Posted on Edited on

安装

sudo apt-get update

sudo apt-get install mysql-server

解决远程连接

tips本人使用环境ubuntu16

完成安装后，远程连接你会发现2003报错，此时，你对 /etc/mysql/mysql.conf.d/ 文件夹中打开 mysqld.cnf文件修改即可

修改内容将#bind-address = 127.0.0.1 原本没有注释，进行注释

然后你重新远程连接mysql直接变成1130的拒绝访问服务，接下来你要在服务器端登录mysql，执行

进入数据库

mysql -u root -p

切换数据库,

mysql>use mysql;

查看root账号的登录权限,

mysql>select host, user from user;

修改登录权限

mysql>update user set host = ‘%’ where user = ‘root’;

刷新,生效,最后一步,至关重要

mysql>flush privileges;

Posted on Edited on In

what is MQ

如果想知道MQ的详细知识可以看我之前的为什么使用消息队列MQ

这里选择最重要的提一下：MQ即消息队列，用来实现程序的异步和解耦，起到消息缓冲，消息分发。通俗来讲就是一个医院（服务器）里面有多个医生（线程或进程），让病人都排队（消息缓冲），有的去A部门，有的去B部门（消息分发）。

成员RabbitMQ

RabbitMQ是实现AMQP（高级消息队列协议Advanced Message Queuing Protocol）的消息中间件的一种，Feature就是组件之间解耦，病人排他的队，医生看他的病人，至于怎么排，医生不用操心，至于怎么看病，病人不用操心，都交给MQ

术语：面向消息，队列，路由（点对点/发布订阅），可靠安全

Posted on Edited on

一下文字摘自JAVA公众号

Linux命令类

tail

最常用的tail -f

1
tail -300f shopbase.log #倒数300行并进入实时监听文件写入模式

grep

1
2
3
4
5
6
7
8
9
10
grep forest f.txt     #文件查找
grep forest f.txt cpf.txt #多文件查找
grep 'log' /home/admin -r -n #目录下查找所有符合关键字的文件
cat f.txt | grep -i shopbase    
grep 'shopbase' /home/admin -r -n --include *.{vm,java} #指定文件后缀
grep 'shopbase' /home/admin -r -n --exclude *.{vm,java} #反匹配
seq 10 | grep 5 -A 3    #上匹配
seq 10 | grep 5 -B 3    #下匹配
seq 10 | grep 5 -C 3    #上下匹配，平时用这个就妥了
cat f.txt | grep -c 'SHOPBASE'

awk

1 基础命令

1
2
3
4
5
6
awk '{print $4,$6}' f.txt
awk '{print NR,$0}' f.txt cpf.txt    
awk '{print FNR,$0}' f.txt cpf.txt
awk '{print FNR,FILENAME,$0}' f.txt cpf.txt
awk '{print FILENAME,"NR="NR,"FNR="FNR,"$"NF"="$NF}' f.txt cpf.txt
echo 1:2:3:4 | awk -F: '{print $1,$2,$3,$4}'

2 匹配

1
2
3
4
awk '/ldb/ {print}' f.txt   #匹配ldb
awk '!/ldb/ {print}' f.txt  #不匹配ldb
awk '/ldb/ && /LISTEN/ {print}' f.txt   #匹配ldb和LISTEN
awk '$5 ~ /ldb/ {print}' f.txt #第五列匹配ldb

3 内建变量

NR:NR表示从awk开始执行后，按照记录分隔符读取的数据次数，默认的记录分隔符为换行符，因此默认的就是读取的数据行数，NR可以理解为Number of Record的缩写。

FNR:在awk处理多个输入文件的时候，在处理完第一个文件后，NR并不会从1开始，而是继续累加，因此就出现了FNR，每当处理一个新文件的时候，FNR就从1开始计数，FNR可以理解为File Number of Record。

NF: NF表示目前的记录被分割的字段的数目，NF可以理解为Number of Field。

find

1
2
3
4
5
6
7
8
9
10
11
12
13
sudo -u admin find /home/admin /tmp /usr -name \*.log(多个目录去找)
find . -iname \*.txt(大小写都匹配)
find . -type d(当前目录下的所有子目录)
find /usr -type l(当前目录下所有的符号链接)
find /usr -type l -name "z*" -ls(符号链接的详细信息 eg:inode,目录)
find /home/admin -size +250000k(超过250000k的文件，当然+改成-就是小于了)
find /home/admin f -perm 777 -exec ls -l {} \; (按照权限查询文件)
find /home/admin -atime -1  1天内访问过的文件
find /home/admin -ctime -1  1天内状态改变过的文件    
find /home/admin -mtime -1  1天内修改过的文件
find /home/admin -amin -1  1分钟内访问过的文件
find /home/admin -cmin -1  1分钟内状态改变过的文件    
find /home/admin -mmin -1  1分钟内修改过的文件

pgm

批量查询vm-shopbase满足条件的日志

1
pgm -A -f vm-shopbase 'cat /home/admin/shopbase/logs/shopbase.log.2017-01-17|grep 2069861630'

tsar

tsar是咱公司自己的采集工具。很好用, 将历史收集到的数据持久化在磁盘上，所以我们快速来查询历史的系统数据。当然实时的应用情况也是可以查询的啦。大部分机器上都有安装。

1
tsar  ##可以查看最近一天的各项指标

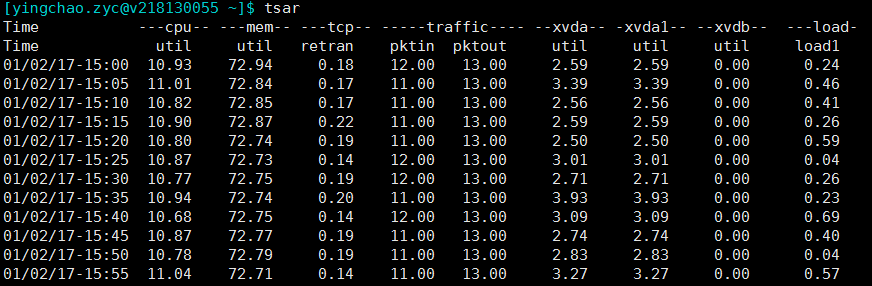
screenshot.png

1
tsar --live ##可以查看实时指标，默认五秒一刷

screenshot.png

1
tsar -d 20161218 ##指定查看某天的数据，貌似最多只能看四个月的数据

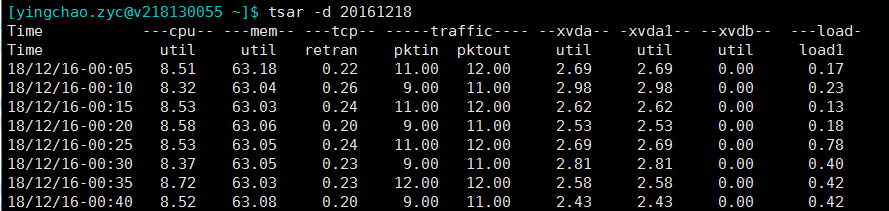
screenshot.png

1
2
3
4
tsar --mem
tsar --load
tsar --cpu
##当然这个也可以和-d参数配合来查询某天的单个指标的情况

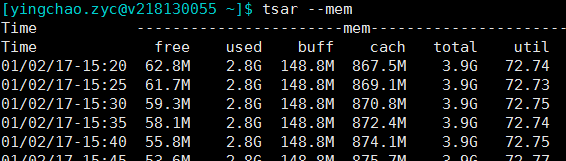
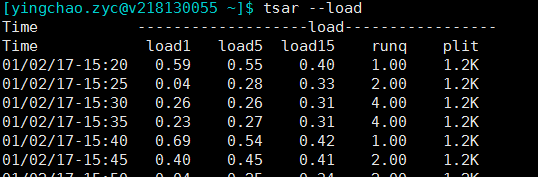
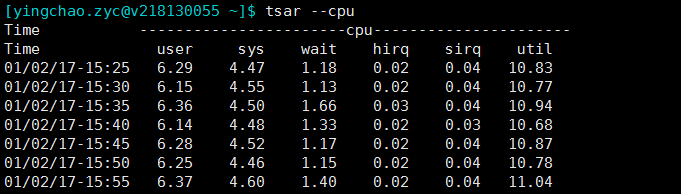
screenshot.png
screenshot.png
screenshot.png

top

top除了看一些基本信息之外，剩下的就是配合来查询vm的各种问题了

1
2
3
ps -ef | grep java
top -H -p pid

获得线程10进制转16进制后jstack去抓看这个线程到底在干啥

其他

1
2
netstat -nat|awk  '{print $6}'|sort|uniq -c|sort -rn 
#查看当前连接，注意close_wait偏高的情况，比如如下

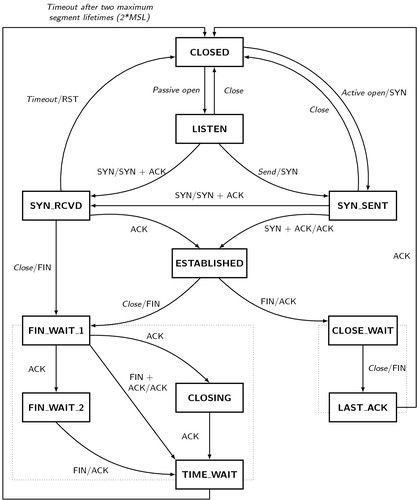
screenshot.png
screenshot.png

排查利器

btrace

首当其冲的要说的是btrace。真是生产环境&预发的排查问题大杀器。 简介什么的就不说了。直接上代码干

  1. 查看当前谁调用了ArrayList的add方法，同时只打印当前ArrayList的size大于500的线程调用栈

    @OnMethod(clazz = “java.util.ArrayList”, method=”add”, location = @Location(value = Kind.CALL, clazz = “/./“, method = “/./“))
    public static void m(@ProbeClassName String probeClass, @ProbeMethodName String probeMethod, @TargetInstance Object instance, @TargetMethodOrField String method) {

    1
    2
    3
    4
    5
    6
    7
    if(getInt(field("java.util.ArrayList", "size"), instance) > 479){
        println("check who ArrayList.add method:" + probeClass + "#" + probeMethod  + ", method:" + method + ", size:" + getInt(field("java.util.ArrayList", "size"), instance));
        jstack();
        println();
        println("===========================");
        println();
    }

    }

  2. 监控当前服务方法被调用时返回的值以及请求的参数

    @OnMethod(clazz = “com.taobao.sellerhome.transfer.biz.impl.C2CApplyerServiceImpl”, method=”nav”, location = @Location(value = Kind.RETURN))
    public static void mt(long userId, int current, int relation, String check, String redirectUrl, @Return AnyType result) {

    1
    println("parameter# userId:" + userId + ", current:" + current + ", relation:" + relation + ", check:" + check + ", redirectUrl:" + redirectUrl + ", result:" + result);

    }

其他功能集团的一些工具或多或少都有，就不说了。感兴趣的请移步。
https://github.com/btraceio/btrace

注意:

  1. 经过观察，1.3.9的release输出不稳定，要多触发几次才能看到正确的结果
  2. 正则表达式匹配trace类时范围一定要控制，否则极有可能出现跑满CPU导致应用卡死的情况
  3. 由于是字节码注入的原理，想要应用恢复到正常情况，需要重启应用。

Greys

Greys是@杜琨的大作吧。说几个挺棒的功能(部分功能和btrace重合):

sc -df xxx: 输出当前类的详情,包括源码位置和classloader结构

trace class method: 相当喜欢这个功能! 很早前可以早JProfiler看到这个功能。打印出当前方法调用的耗时情况，细分到每个方法。对排查方法性能时很有帮助，比如我之前这篇就是使用了trace命令来的:http://www.atatech.org/articles/52947。

其他功能部分和btrace重合，可以选用，感兴趣的请移步。
http://www.atatech.org/articles/26247

另外相关联的是arthas，他是基于Greys的，感兴趣的再移步http://mw.alibaba-inc.com/products/arthas/docs/middleware-container/arthas.wiki/home.html?spm=a1z9z.8109794.header.32.1lsoMc

javOSize

就说一个功能
classes：通过修改了字节码，改变了类的内容，即时生效。 所以可以做到快速的在某个地方打个日志看看输出，缺点是对代码的侵入性太大。但是如果自己知道自己在干嘛，的确是不错的玩意儿。

其他功能Greys和btrace都能很轻易做的到，不说了。

可以看看我之前写的一篇javOSize的简介http://www.atatech.org/articles/38546
官网请移步http://www.javosize.com/

JProfiler

之前判断许多问题要通过JProfiler，但是现在Greys和btrace基本都能搞定了。再加上出问题的基本上都是生产环境(网络隔离)，所以基本不怎么使用了，但是还是要标记一下。
官网请移步https://www.ej-technologies.com/products/jprofiler/overview.html

大杀器

eclipseMAT

可作为eclipse的插件，也可作为单独的程序打开。
详情请移步http://www.eclipse.org/mat/

zprofiler

集团内的开发应该是无人不知无人不晓了。简而言之一句话:有了zprofiler还要mat干嘛
详情请移步zprofiler.alibaba-inc.com

java三板斧，噢不对，是七把

jps

我只用一条命令：

1
sudo -u admin /opt/taobao/java/bin/jps -mlvV

screenshot.png

jstack

普通用法:

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jstack 2815

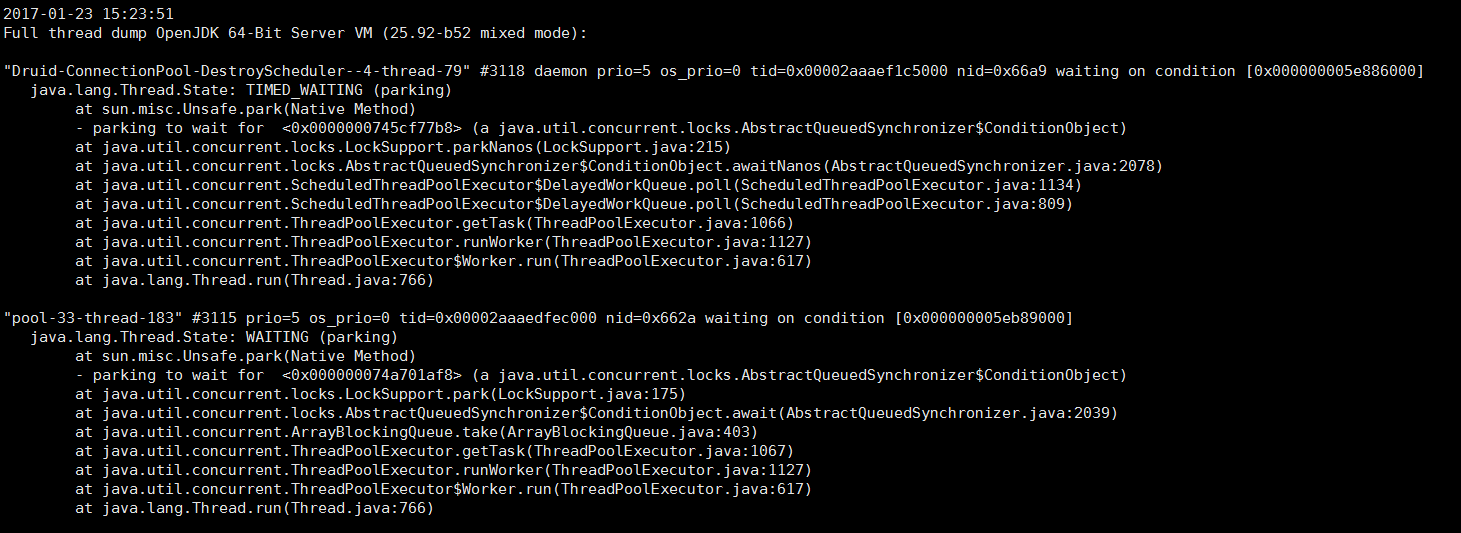
screenshot.png

native+java栈:

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jstack -m 2815

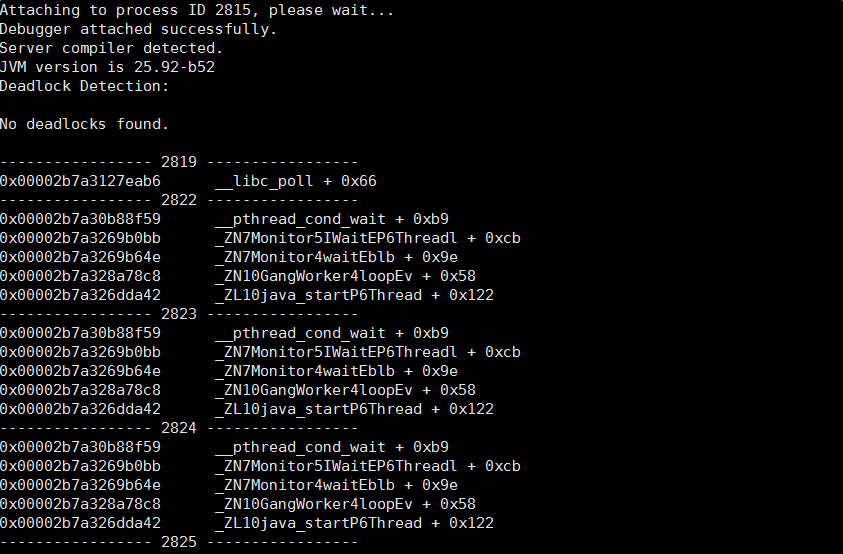
screenshot.png

jinfo

可看系统启动的参数，如下

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jinfo -flags 2815

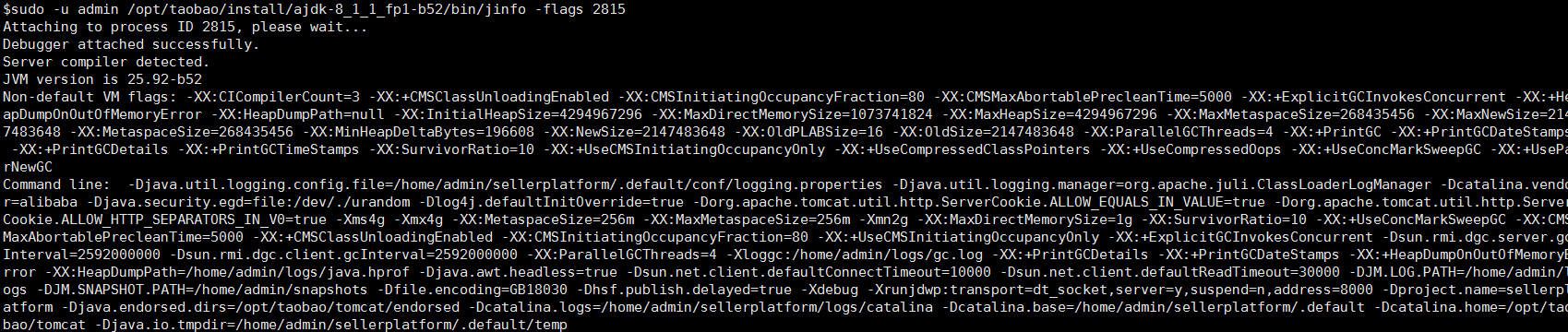
screenshot.png

jmap

两个用途

1.查看堆的情况

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jmap -heap 2815

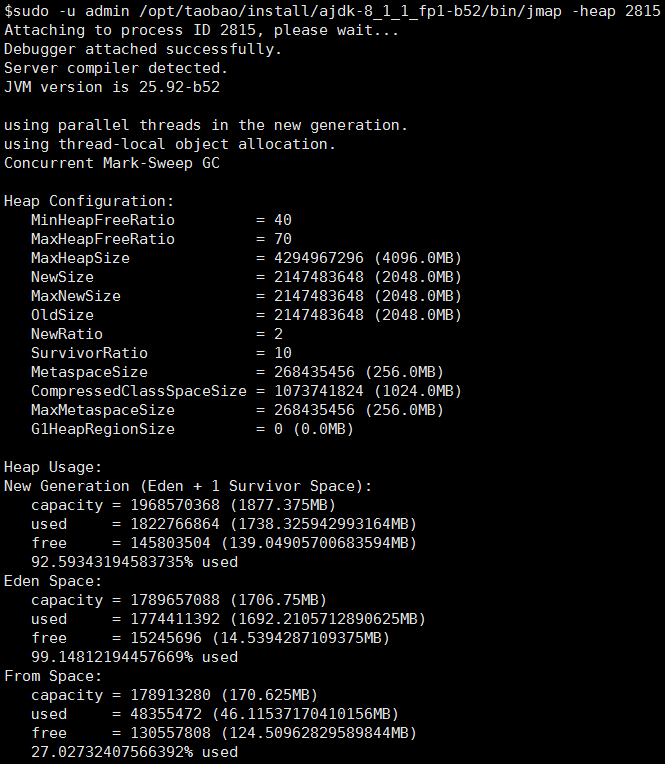
screenshot.png
screenshot.png

2.dump

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jmap -dump:live,format=b,file=/tmp/heap2.bin 2815

或者

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jmap -dump:format=b,file=/tmp/heap3.bin 2815

3.看看堆都被谁占了? 再配合zprofiler和btrace，排查问题简直是如虎添翼

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jmap -histo 2815 | head -10

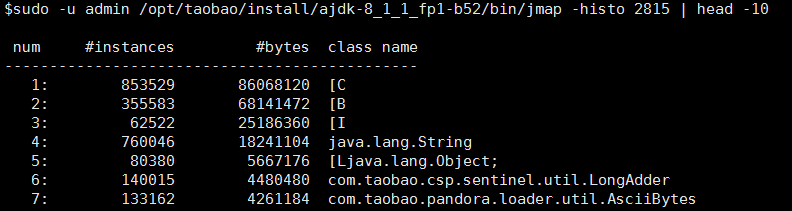
screenshot.png

jstat

jstat参数众多，但是使用一个就够了

1
sudo -u admin /opt/taobao/install/ajdk-8_1_1_fp1-b52/bin/jstat -gcutil 2815 1000

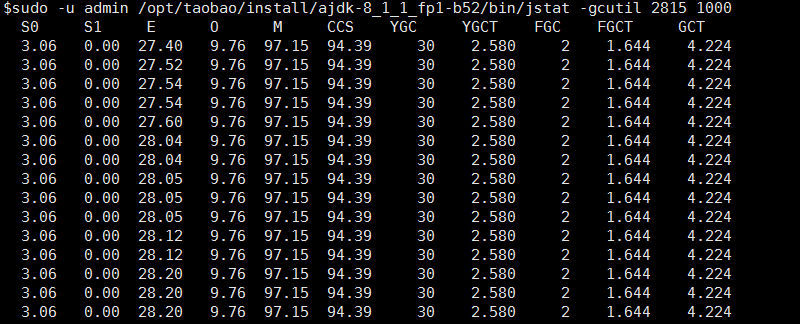
screenshot.png

jdb

时至今日，jdb也是经常使用的。
jdb可以用来预发debug,假设你预发的java_home是/opt/taobao/java/，远程调试端口是8000.那么
sudo -u admin /opt/taobao/java/bin/jdb -attach 8000.

screenshot.png

出现以上代表jdb启动成功。后续可以进行设置断点进行调试。
具体参数可见oracle官方说明http://docs.oracle.com/javase/7/docs/technotes/tools/windows/jdb.html

CHLSDB

CHLSDB感觉很多情况下可以看到更好玩的东西，不详细叙述了。 查询资料听说jstack和jmap等工具就是基于它的。

1
sudo -u admin /opt/taobao/java/bin/java -classpath /opt/taobao/java/lib/sa-jdi.jar sun.jvm.hotspot.CLHSDB

更详细的可见R大此贴
http://rednaxelafx.iteye.com/blog/1847971

plugin of intellij idea

key promoter

快捷键一次你记不住，多来几次你总能记住了吧？

screenshot.png

maven helper

分析maven依赖的好帮手。

VM options

  1. 你的类到底是从哪个文件加载进来的？

    1
    2
    3
    -XX:+TraceClassLoading
    结果形如[Loaded java.lang.invoke.MethodHandleImpl$Lazy from D:\programme\jdk\jdk8U74\jre\lib\rt.jar]

  2. 应用挂了输出dump文件

    1
    2
    -XX:+HeapDumpOnOutOfMemoryError -XX:HeapDumpPath=/home/admin/logs/java.hprof
    集团的vm参数里边基本都有这个选项

jar包冲突

把这个单独写个大标题不过分吧？每个人或多或少都处理过这种烦人的case。我特么下边这么多方案不信就搞不定你?

mvn dependency:tree > ~/dependency.txt

打出所有依赖

mvn dependency:tree -Dverbose -Dincludes=groupId:artifactId

只打出指定groupId和artifactId的依赖关系

-XX:+TraceClassLoading

vm启动脚本加入。在tomcat启动脚本中可见加载类的详细信息

-verbose

vm启动脚本加入。在tomcat启动脚本中可见加载类的详细信息

greys:sc

greys的sc命令也能清晰的看到当前类是从哪里加载过来的

tomcat-classloader-locate

通过以下url可以获知当前类是从哪里加载的
curl http://localhost:8006/classloader/locate?class=org.apache.xerces.xs.XSObject

ALI-TOMCAT带给我们的惊喜(感谢@务观)

  1. 列出容器加载的jar列表

    curl http://localhost:8006/classloader/jars

  2. 列出当前当当前类加载的实际jar包位置，解决类冲突时有用

    curl http://localhost:8006/classloader/locate?class=org.apache.xerces.xs.XSObject
    screenshot.png

其他

gpref

http://www.atatech.org/articles/33317

dmesg

如果发现自己的java进程悄无声息的消失了，几乎没有留下任何线索，那么dmesg一发，很有可能有你想要的。

1
sudo dmesg|grep -i kill|less

去找关键字oom_killer。找到的结果类似如下:

1
2
3
4
5
[6710782.021013] java invoked oom-killer: gfp_mask=0xd0, order=0, oom_adj=0, oom_scoe_adj=0
[6710782.070639] [<ffffffff81118898>] ? oom_kill_process+0x68/0x140 
[6710782.257588] Task in /LXC011175068174 killed as a result of limit of /LXC011175068174 
[6710784.698347] Memory cgroup out of memory: Kill process 215701 (java) score 854 or sacrifice child 
[6710784.707978] Killed process 215701, UID 679, (java) total-vm:11017300kB, anon-rss:7152432kB, file-rss:1232kB

以上表明，对应的java进程被系统的OOM Killer给干掉了，得分为854.
解释一下OOM killer（Out-Of-Memory killer），该机制会监控机器的内存资源消耗。当机器内存耗尽前，该机制会扫描所有的进程（按照一定规则计算，内存占用，时间等），挑选出得分最高的进程，然后杀死，从而保护机器。

dmesg日志时间转换公式:
log实际时间=格林威治1970-01-01+(当前时间秒数-系统启动至今的秒数+dmesg打印的log时间)秒数：

1
date -d "1970-01-01 UTC `echo "$(date +%s)-$(cat /proc/uptime|cut -f 1 -d' ')+12288812.926194"|bc ` seconds"

剩下的，就是看看为什么内存这么大，触发了OOM-Killer了。

新技能get

RateLimiter

想要精细的控制QPS? 比如这样一个场景，你调用某个接口，对方明确需要你限制你的QPS在400之内你怎么控制？这个时候RateLimiter就有了用武之地。详情可移步http://ifeve.com/guava-ratelimite

Posted on Edited on In

problem

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

Example 1:

1
2
3
Input: [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

1
2
3
4
Input: [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
             jump length is 0, which makes it impossible to reach the last index.

key

本题有两个易理解错的地方

  • 达到最后一个index或者超过最后一个index是可以的
  • 【2,5,0,0】第一个2可以跳两步，然后我们在5的基础上跳五步

本题采用贪心算法，算出局部最优解就可以了，当然也可以考虑dp，但本题没有这个必要

solution

1
2
3
4
5
6
public boolean canJump(int[] nums) {
		int reach = nums[0];
        for(int i = 1; i < nums.length && reach >= i; i++)
            if(i + nums[i] > reach) reach = i + nums[i];
        return reach >= (nums.length-1) ? true : false;
	}

perfect

1
I'm the perfect

Posted on Edited on In

54.problem

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

1
2
3
4
5
6
7
Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

1
2
3
4
5
6
7
Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

key

很简单的循环输出的例子，从【0,0】的位置顺时针扫一圈，然后缩小一圈，继续扫描，不过有一个细节就是第三次第四循环前，要判断一下,防止最后一层循环只有一行

solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public List<Integer> spiralOrder(int[][] matrix) {

		List<Integer> ans = new ArrayList<Integer>();
		if (matrix.length == 0)
			return ans;
		int rs = 0, re = matrix.length - 1;// rowStart rowEnd
		int cs = 0, ce = matrix[0].length - 1;// columnStart columnEnd
		while (rs <= re && cs <= ce) {
			for (int i = cs; i <= ce; i++) {
				ans.add(matrix[rs][i]);
			}
			for(int j=rs+1;j<=re;j++) {
				ans.add(matrix[j][ce]);
			}
			if(rs<re&&cs<ce) {
				for(int k=ce-1;k>cs;k--) {
					ans.add(matrix[re][k]);
				}
				for(int l=re;l>rs;l--) {
					ans.add(matrix[l][cs]);
				}
			}
			
			rs++;
			re--;
			cs++;
			ce--;
		}
		return ans;
	}

perfect

1
yehh,I'm the perfect

Posted on Edited on In

solution

source 下放置32*32的favico.icon文件并在根目录的_config.yml中设置

favicon: /favicon.ico

Posted on Edited on In

problem

很多人可能都有hexo博客，会有一个githubname.github.io的地址，然后自己可能想去买一个域名，方便记忆，但是解析后迟迟用不了，该文章就来详细描述一下步骤。

solution

1.拥有一个githubname.github.io可以正常访问的域名，如我的GitHub博客：https://shawngoethe.github.io

2.购买域名，个人推荐阿里云，首年年费比较便宜，适合个人折腾，博客建议com,me,info,pro（专家）,mobi(kindle电子书的格式)，再不济可以选择tech，cc之类的，国外可以参考Linost之类的网页

3.购买域名进行实名认证，否则无法使用

4.进行解析：记录类型CNAME（进行转发），主机记录@（避免主机记录选择www，输入域名要多写www），记录值为shawngoethe.github.io,TTL选择10分钟就可以了

上述方法属于将我购买的zehai.info转发到了shawngoethe.github.io,还可以“记录类型”选择“A”来填写IPv4的地址，地址可以通过ping shawngoethe.github.io 来获得

5.修改代码：很多人忽视了要在源代码/hexoblog/source/目录下添加CNAME文件（注意没有尾缀），然后在该文件下填写zehai.info（可以兼容，www.zehai.info 和 zehai.info 两种访问方式，但如果填写 www.zehai.info 则只支持 www.zehai.info 一种访问方式）

6.等十分钟左右，让解析生效，好了，你可以访问我的hexo获取更多内容

Posted on Edited on In

problem

Maximum Subarray

Easy

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

1
2
3
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

key

我们定义一个和为第一位数，然后用curSum来保存递增量

ps ans–>answer cur–>cursor

solution

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxSubArray(int[] nums) {
        int ans=nums[0], curSum=0;
        
        for (int i=0; i<nums.length; i++) {
            curSum = curSum + nums[i];
            ans = Math.max(ans, curSum);
            curSum = Math.max(0, curSum);
        }
        
        return ans;
    }
}

perfect

1
2
3
4
5
6
7
8
9
10
class Solution {
    public int maxSubArray(int[] nums) {
        int dp = nums[0], maxSum=nums[0];
        for (int i=1; i<nums.length; i++) {
            dp = dp<0?nums[i]:nums[i]+dp;
            maxSum=Math.max(maxSum, dp);
        }
        return maxSum;
    }
}

Posted on Edited on In

problem

\50. Pow(x, n)

Medium

Implement pow(x, n), which calculates x raised to the power n (xn).

Example 1:

1
2
Input: 2.00000, 10
Output: 1024.00000

Example 2:

1
2
Input: 2.10000, 3
Output: 9.26100

Example 3:

1
2
3
Input: 2.00000, -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Note:

  • -100.0 < x < 100.0
  • n is a 32-bit signed integer, within the range [−231, 231 − 1]

solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public double myPow(double x, int n) {

		long N = n;
		if (N < 0) {
			x = 1 / x;
			N = -N;
		}

		double ans = 1;
		double cur = x;//2
		for (long i = N; i > 0; i /= 2) {
			if (i % 2 == 1)
				ans = ans * cur;
			cur = cur * cur;
		}
		return ans;

	}
//偷懒方法
public double myPow(double x, int n) {
		return Math.pow(x, n);
	}

key

其实先使用了偷懒的方法，调用Math库的pow方法，然后写过一版

1
2
3
for(long i=N;i>0;i--) {
	ans=ans*cur;
}

这个会直接报超时的错误，因为的计算量会非常大，在计算（-1.00000，-2147483648）时候超时了，虽然我们可以通过判断x来避免这一个超时，但是我想到了，可以通过n/2来迅速减少相乘的次数。时间大概是8ms

perfect

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public double findPower(double x,long n){
        if(n == Long.valueOf(1))
            return x;
        if(n % 2 == 0){
            double half_pow = findPower(x,n/2);
            return half_pow * half_pow;
        }else{
            double half_pow = findPower(x,(n-1)/2);
            return half_pow * half_pow * x;
        }
        
    }
    public double myPow(double x, int n) {
            if( n==0 )
                return 1;
         
            long n_long = (long) n;
            if( n > 0 )
                return findPower(x,n);
            
            x = 1 / x;
            long n_long_abs =  (long) Math.abs((long)n);
            if(n_long_abs == 1)
                return x;
            return findPower(x,n_long_abs);
    }
}

Posted on Edited on In

我在一个不属于我的地方游荡

2019年的3月6日，距离我上一份工作离职，已经37天，日子过得虽然不好，但也不算差，好消息是阿len还陪着我，坏消息是一直过着异地恋的生活，不知道是为什么，是我进入了焦虑的状态，每天的日常就是投简历，思考人生，发呆，看up主秀恩爱

其实回顾前三次的找工作经历，哪次不是觉得自己快要变成咸鱼了，然后收到了一两个offer，不过今年的不同点就是，有三家，我已经过了用人单位的面试，却被卡在了人力资源部门的审核上，我时常恨自己的学历，却无法去原谅曾经高考的自己，写这篇文章的时候，我刚刚从清华的北门进入校园，下午两点半的宿舍区，没有一点噪音，天空的乌鸦鸣叫在空旷的校园回荡，仿佛，在感叹今日的好天气，阳光那么明亮，洒在光秃秃的树枝上。

1552225241907

17年考研复习期间埋下来的雷，最终还是爆炸了，18年，19年，20年，似乎时间过得很快，我丢失了那一次机会后，我似乎再也没有机会去投入身心去复习，每天的大脑里更多的是，好累啊，好烦啊，什么时候发工资啊。越生是怀念起无忧无虑的本科生活，天天不用担心我是谁，我在哪儿，学什么，可能唯一需要费点脑经的就是，中午吃啥

1552225254472

而现在，我走在一个不属于我的世界里，熟悉又陌生，我什么都不知道，因为我不知道我要干嘛，前方一个是找不到工作的工作方向，一个是会饿死的考研方向，世界很精彩，我却显得那么渺小，就深深想起来用人部门发信息和我说：

从技术层面上，我认为从工作年限上，你的水平是够的。对于候选人的学历背景上，央企有自身的痼疾，用人部门的话语权不一定大于人力部门，这个你也无须介怀。

工作的前三年对于一个工程师来说是至关重要的，如果喜欢这条路，就多花点时间，加油！江湖不大，有缘再见！

不知道接下来应该做什么，或许这就是应试教育的悲哀，我也只能许愿，三月份能够拿到一个不错的offer，先活下来，我是子苏，一个快要得抑郁症的人。

0%